Contents
- Two Types of Security
- Polynomial Interpolation - An Unbreakable Security
- Security Proofs
- Why Quantum Computers Can't Break Information-Theoretic Security
- Inherited Immunity: Building Quantum-Resistant Systems with Thresholds
- Comparing SSS to traditional cryptography under quantum threat
- Practical considerations and implementation challenges
- SSS and Post-Quantum Cryptography: A Hybrid Defense
- A Timeless Solution for a Future Threat
Shamir's Secret Sharing (SSS) for Quantum-Safe Data Storage
How does Shamir's Secret Sharing (SSS) provide you with Quantum-safe data protection?
In our previous article, Quantum Supremacy: Is it a Real Threat?, we explored how quantum computers pose existential threats to modern cryptography. RSA, elliptic curve cryptography, and most encryption systems that protect our digital world today rely on computational problems that quantum algorithms can solve exponentially faster than classical computers.
However, there is still a mathematical approach that remains unshaken by quantum advances. Shamir's Secret Sharing (SSS) is a secret distribution or key-splitting scheme. It’s based on classical information theory and polynomial interpolation, not number-theoretic assumptions (like factoring or discrete log) that quantum computers break.
Due to this, it is not directly affected by quantum attacks, like Shor’s algorithm.
Two Types of Security
Most cryptography today relies on computational security. This means the system is secure as long as certain mathematical problems remain hard to solve within reasonable time limits. RSA depends on the difficulty of factoring large integers. Elliptic curve cryptography relies on the complexity of the discrete logarithm problem. These assumptions work well against classical computers but fail under quantum algorithms like Shor's algorithm.
Information-theoretic security takes a completely different approach. Instead of relying on computational hardness, it achieves security through mathematical impossibility. When Claude Shannon introduced this concept in 1949, he proved that some systems can be mathematically proven secure against any attacker, regardless of their computational power.
The one-time pad is the classic example. If an encryption key is truly random, as long as the message is, and is used only once, it's mathematically impossible to crack. This holds up even with infinite computing power. An attacker looking at the encrypted message sees only random data, with no way to distinguish the correct decryption from any other possible message of the same length.
Shamir's Secret Sharing achieves this same level of mathematical certainty through a different mechanism: polynomial mathematics.
Polynomial Interpolation - An Unbreakable Security
Adi Shamir's 1979 breakthrough is built on a fundamental property of polynomials: you need exactly N points to determine a polynomial of degree N-1 uniquely. If that sounds unfamiliar, recall your high school geometry: any straight line is uniquely determined by two points. With only one point, infinitely many lines can pass through it. This is the principle behind the most common Shamir threshold in practice: the 2-of-3 scheme. Here, N is 2, so the polynomial is of the first degree, which is an equation for a straight line. This simple mathematical fact is the foundation for a security model that is not only provable, but also inherently quantum-resistant. It means that if an attacker has only one share (the coordinates of a single point), they cannot possibly reconstruct the secret "line". As a result, there are infinitely many equally plausible secrets for them to consider.
Below is a basic example of the concept outlined above:
- Secret S = 6. Pick a random line → y = 5x + 6
- Creation of two shares:
- First at x = 1 → y = 11 → (1, 11);
- Second at x = 3 → y = 21 → (3, 21).
- Reconstruct:
- Slope a = (21 − 11) / (3 − 1) = 5;
- Then y = 5x + b, plug x = 1, y = 11 → b = 6.
- The secret is the value at x = 0: y(0) = 6 — recovered.
Here is a more complex formulas of t-of-n generalized case:
Secret as the value at zero of a degree (t−1) polynomial: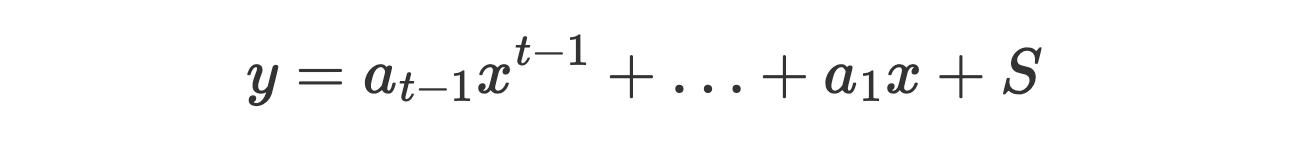
Shares generation: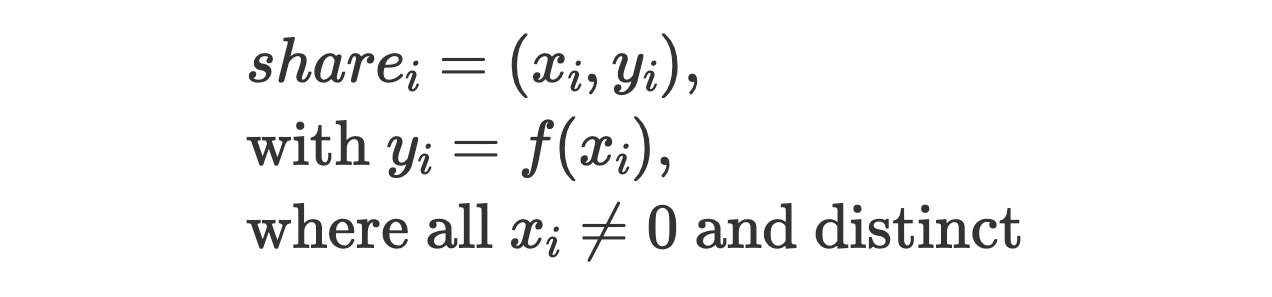
Reconstruction of secret (Lagrange at x=0):
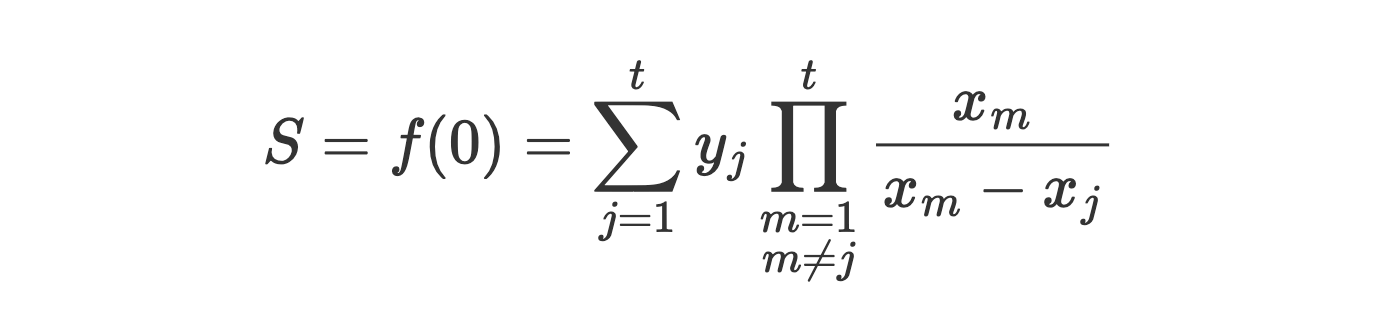
Security Proofs
With only t-1 shares, you have t-1 equations but t unknowns (the t coefficients of the polynomial). In linear algebra, this system has an infinite number of solutions. Every possible secret value is equally likely given the available information.
This isn't a computational limitation - it's a mathematical impossibility. Even knowing t-1 shares perfectly, an attacker with quantum computers and unlimited time cannot determine which of the infinite possible secrets is correct.
Why Quantum Computers Can't Break Information-Theoretic Security
Quantum computers excel at certain types of problems through quantum properties like superposition and entanglement. Shor's algorithm can factor integers exponentially faster than classical computers. Grover's algorithm can search unsorted databases with quadratic speedup.
But quantum computers cannot violate fundamental mathematical constraints. If a polynomial of degree t-1 requires t points for unique determination, no amount of quantum computation can extract more information from fewer points. The security of Shamir's Secret Sharing isn't based on computational difficulty - it's based on mathematical impossibility.
This creates an interesting paradox: while quantum computers will break RSA, AES, and elliptic curve systems that protect most of our digital infrastructure, they remain powerless against a scheme invented in 1979 using classical mathematics.
Inherited Immunity: Building Quantum-Resistant Systems with Thresholds
The quantum resistance of Shamir's Secret Sharing is not just a feature of the algorithm itself. It is also a property that can be inherited by any system built upon it. This makes SSS a powerful foundation for creating complex, quantum-resilient security models based on distributed trust.
At its core, a (t,n) threshold scheme is more than just a way to split a secret. It's a mechanism for distributing authority and eliminating single points of failure. When a larger system uses SSS to protect a critical secret, that system's core secret management layer inherits the information-theoretic security of SSS. This allows for the design of sophisticated, quantum-resistant access control systems.
This approach excels at protecting high-value secrets that need long-term protection and distributed access control, such as:
- Fault-proof backups of cryptocurrency wallet seed phrases and private keys.
- Protecting certificate authority root keys.
- Securing database encryption keys.
- Guarding corporate trade secrets and intellectual property.
- Military & Critical Infrastructure secrets, like nuclear launch codes.
Comparing SSS to traditional cryptography under quantum threat
| Aspect | Traditional Crypto | Shamir's Secret Sharing |
|---|---|---|
| Security basis | Computational hardness | Mathematical impossibility |
| Quantum vulnerability | Vulnerable to Shor's algorithm | Quantum-immune |
| Key management | Single points of failure | Distributed trust |
| Performance impact | Quantum attacks reduce security | No impact from quantum advances |
| Future-proofing | Requires algorithm updates | Inherently future-proof |
Practical considerations and implementation challenges
While SSS is theoretically perfect, its real-world implementation requires careful design:
- Secure Share Distribution: The shares themselves must be distributed and stored securely. If you use a quantum-vulnerable channel to send a share, the system's overall security could be compromised. This is why protocols like the hardened open-source Zax relay are critical for transport.
- Protecting the Shares: Each share must be protected from theft or loss. Encrypting shares with traditional algorithms can reintroduce a quantum vulnerability. A better approach is to utilize hardware security, like a smartphone's Secure Enclave, to protect shares at rest, as the Vault12 Guard app does.
- Secure Secret Usage: SSS secures a secret at rest. Once reconstructed, the secret must also be used securely. In Bitcoin, for maximum quantum resilience, it is recommended to use Taproot addresses (starting with `bc1p`), as their 256-bit key structure offers stronger protection against quantum search algorithms than the 160-bit hashes of older address types. Most importantly, never reusing addresses is a critical security practice. After any funds are spent from an address, its public key is exposed, making it a potential target for a quantum threat.
SSS and Post-Quantum Cryptography: A Hybrid Defense
The race to standardize post-quantum cryptography (PQC) is well underway, led by institutions like NIST. This effort has produced a new generation of algorithms designed to withstand quantum attacks, such as CRYSTALS-Kyber (for key encapsulation) and CRYSTALS-Dilithium (for digital signatures). Alongside these, other robust primitives such as the hash-based signature scheme SPHINCS+ (specified in IETF RFC 8391) offer proven assistance in conservative security.
However, it's crucial to understand that these new PQC algorithms, while powerful, still operate on the principle of computational security. They are based on mathematical problems believed to be hard for both classical and quantum computers. They represent the next frontier in a long-running arms race, but do not offer a completion of this race.
This is where Shamir's Secret Sharing provides a perfect, complementary layer of defense. SSS does not compete with PQC; it partners with it to create a truly hybrid, defense-in-depth architecture.
You can use PQC algorithms for what they do best: securing data in transit, authentication, and digital signatures. Then, you can utilize SSS to protect the ultimate "keys to the kingdom" at rest. This creates a powerful hybrid model: even if future theoretical or computational breakthroughs were to crack today's PQC standards, the core secret protected by SSS would remain secure due to its information-theoretic guarantee. It's the ultimate backstop in an uncertain future.
A Timeless Solution for a Future Threat
As quantum computing advances, organizations require cryptographic strategies that provide both immediate protection and long-term security guarantees. SSS offers a unique value proposition: mathematical certainty in an uncertain technological future.
In our next article, "Building Quantum-Resistant Apps with Capacitor", we'll explore practical implementation strategies for integrating SSS into modern applications. We'll cover the Capacitor plugin ecosystem, performance optimization techniques, and real-world deployment patterns that combine theoretical security guarantees with practical usability.
The quantum threat is real and approaching; however, with mathematical tools like Shamir's Secret Sharing, we can build systems that remain secure regardless of future technological advances. The mathematics that Shamir discovered in 1979 provides a timeless foundation for security in the quantum age.
Shamir's Secret Sharing (SSS) for Quantum-Safe Data Storage
How does Shamir's Secret Sharing (SSS) provide you with Quantum-safe data protection?

Art Krotou
Art is a crypto-security expert and researcher with serial entrepreneurship background. Having a degree in physics and experiences in multiple cutting-edge industries like fintech, secure hardware and semiconductors, and identity gave him a unique multi-faceted perspective on the problem of key management for individuals in the crypto networks and the evolution of the internet in general.
In his current work, he is specifically researching how cryptographic keys can be inherited without posing a threat to 3rd parties in edge cases. In addition, he advocates for "fault-tolerance via secrets automation". He discusses the quantitative impact of user experience factors on the uptake of non-custodial solutions.
As one of his most notable accomplishments, he co-founded and led through the early years of the company that contributed to the complex technology behind Apple's recent M-series CPUs. He is also the creator of the most friendly and aesthetically pleasing, but nonetheless super secure and fault-tolerant hardware wallet - U•HODL.
Check out his curated series of "Vault12 Learn" contributions below, and follow him on Twitter and LinkedIn for more sharp insights.

Vault12
Vault12 is the pioneer in crypto inheritance and backup. The company was founded in 2015 to provide a way to enable everyday crypto customers to add a legacy contact to their cry[to wallets. The Vault12 Guard solution is blockchain-independent, runs on any mobile device with biometric security, and is available in Apple and Google app stores.
Vault12 is NOT a financial institution, cryptocurrency exchange, or custodian. We do NOT hold, transfer, manage, or have access to any user funds, tokens, cryptocurrencies, or digital assets. Vault12 is exclusively a non-custodial information security and backup tool that helps users securely store their own wallet seed phrases and private keys for the purpose of inheritance. We provide no legal or financial services, asset management, transaction capabilities, or investment advice. Users maintain complete control of their assets at all times.
You will lose your Bitcoin and other crypto when you die...
...unless you set up Crypto Inheritance today.
It's simple — if you don't worry about crypto inheritance, nobody else will — not your software or hardware wallet vendors, not your exchanges, and not your wealth managers. So it's up to you to think about how to protect the generational wealth you have created, and reduce the risks around passing that crypto wealth on to your family and heirs. What are the challenges with crypto inheritance?
- Crypto Wallets are difficult to use and do not offer crypto inheritance management. In fact, most of them tell you to write down your seed phrase on a piece of paper, which is practically useless.
- Some people back up their wallet seed phrases or private keys on paper, local devices like hardware wallets or USBs, or in the cloud. All of these options have severe drawbacks that range from hacking to accidental loss to disrupted cloud services.
- Software wallets operate on specific blockchains, yet your crypto assets span multiple blockchains. For inheritance to work, you must be able to manage inheritance across every blockchain — now and forever.
Pioneering Crypto Inheritance: Secure Quantum-safe Storage and Backup
Vault12 is the pioneer in Crypto Inheritance, offering a simple yet powerful way to designate a legacy contact and pass on your crypto assets—like Bitcoin (BTC), Ethereum (ETH) and Solana (SOL) —to future generations. Built for everyday users yet robust enough for the most seasoned crypto enthusiasts, Vault12 Guard ensures your wallet seed phrases and private keys are preserved in a fully self-sovereign manner, across all Blockchains.
At the heart of Vault12 Guard is quantum-resistant cryptography and a decentralized, peer-to-peer network of trusted Guardians. Your critical information is never stored in the cloud, on Vault12 servers, or even on local devices—dramatically reducing the risk of a single point of failure. By fusing a powerful software layer with the Secure Element of iOS devices (Secure Enclave) and Google devices (Strongbox), Vault12 Guard locks down your private keys against present and future threats.
Our innovative approach harnesses social recovery, enabling you to appoint one or more trusted individuals or mobile devices as Guardians. These Guardians collectively safeguard your protected seed phrases in a decentralized digital Vault—so there’s no need for constant lawyer updates or bulky paperwork. Should the unexpected happen, your chosen legacy contact can seamlessly inherit your crypto assets without compromising your privacy or security.
Preserve your digital wealth for generations to come with Vault12 Guard—the simplest, most secure way to manage crypto inheritance and backup.
Take the first step and back up your crypto wallets.
Designed to be used alongside traditional hardware and software crypto wallets, Vault12 Guard helps cryptocurrency owners back up their wallet seed phrases and private keys (assets) without storing anything in the cloud, or in any single location. This increases protection and decreases the risk of loss.
The first step in crypto Inheritance Management is making sure you have an up-to-date backup.
The Vault12 Guard app enables secure decentralized backups, and provides inheritance for all your seed phrases and private keys across any blockchain, including Bitcoin, Ethereum, and others, and for any crypto wallet.
Note: For anyone unfamiliar with cryptocurrencies, Vault12 refers to wallet seed phrases and private keys as assets, crypto assets, and digital assets. The Vault12 Guard app includes a software wallet that works alongside your Digital Vault. The primary purpose of this is to guard your Bitcoin (BTC) and Ethereum (ETH) wallet seed phrases, private keys, and other essential data, now and for future generations.